Concave Up Or Down: A Comprehensive Guide To Understanding The Concept

When it comes to mathematics and graph analysis, the terms "concave up or down" play a pivotal role in describing the behavior of curves and functions. These terms aren't just restricted to academic environments; they have practical applications in physics, economics, and even engineering. Understanding whether a curve is concave up or down helps us interpret data trends, optimize functions, and predict outcomes more effectively.

In simpler terms, "concave up or down" refers to the curvature of a graph. If a curve bends upward like a bowl, it is termed concave up. Conversely, if it bends downward like a dome, it is called concave down. This property is often linked to the second derivative of a function, which helps identify the nature of curvature and its implications. Moreover, this concept aids in understanding critical points like maxima, minima, and points of inflection, providing a clearer picture of the graph's behavior.

So, why does this matter? Well, whether you're a student trying to ace your calculus exam or a professional analyzing data trends, grasping the essence of "concave up or down" is indispensable. This article will delve into the intricacies of this mathematical concept, break it down into digestible chunks, and explore its applications, examples, and relevance across multiple domains. Let’s get started and make this concept as clear as possible!

Read also:

All About Reality Tea Latest Trends And Insights

Table of Contents

• What Does Concave Up or Down Mean?
• Why Is Concave Up or Down Important?
• How to Determine Concave Up or Down?
• The Role of the Second Derivative
• Examples of Concave Up and Concave Down
• Applications in Economics
• Applications in Physics
• Applications in Engineering
• Real-World Illustrations
• Common Misconceptions
• How Do Inflection Points Relate to Concavity?
• How to Change Concavity?
• Frequently Asked Questions
• Conclusion

What Does Concave Up or Down Mean?

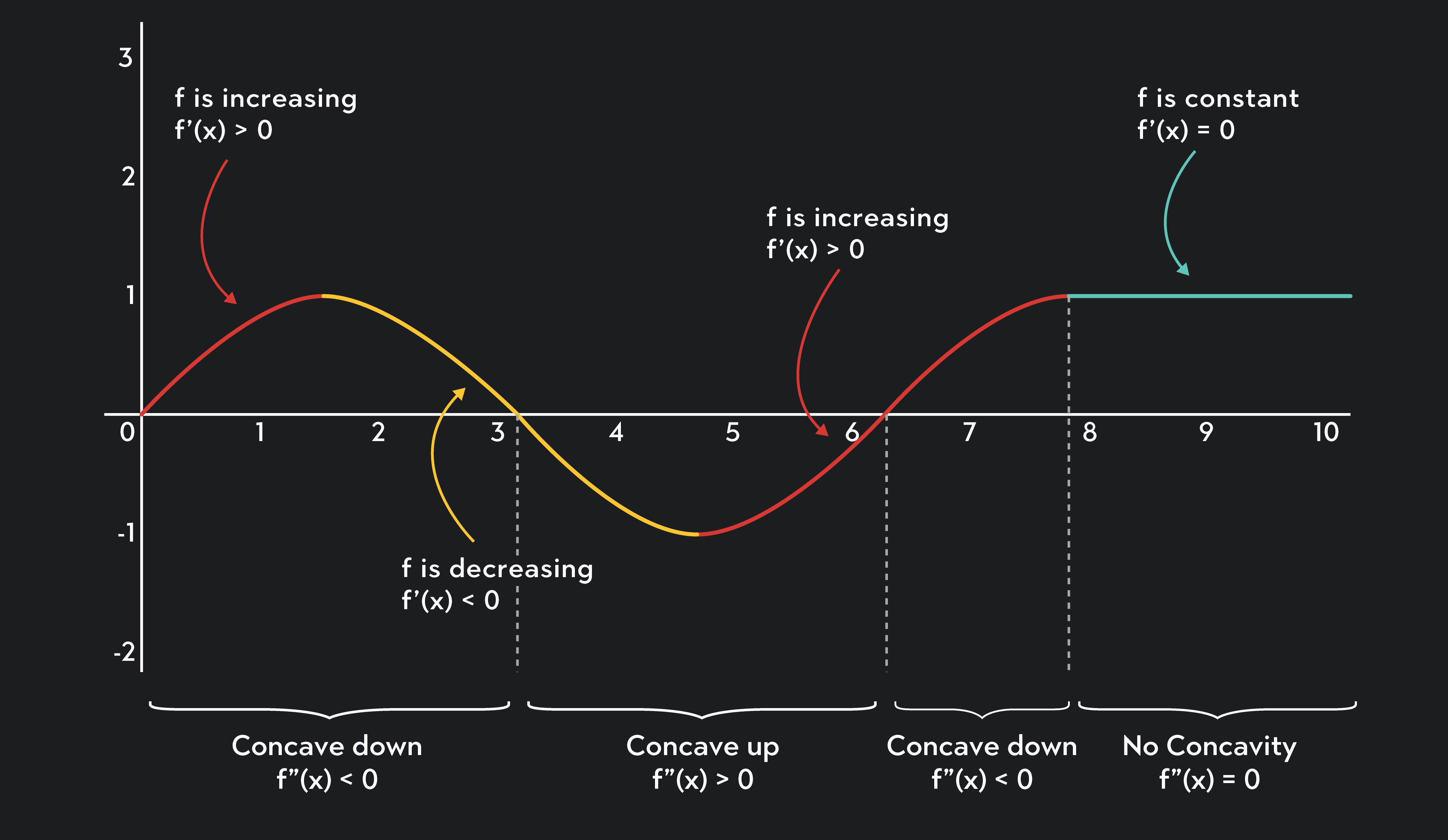
In the simplest terms, a curve's concavity describes its direction of bending. When we talk about "concave up or down," we're referring to whether the graph of a function bends upwards or downwards.

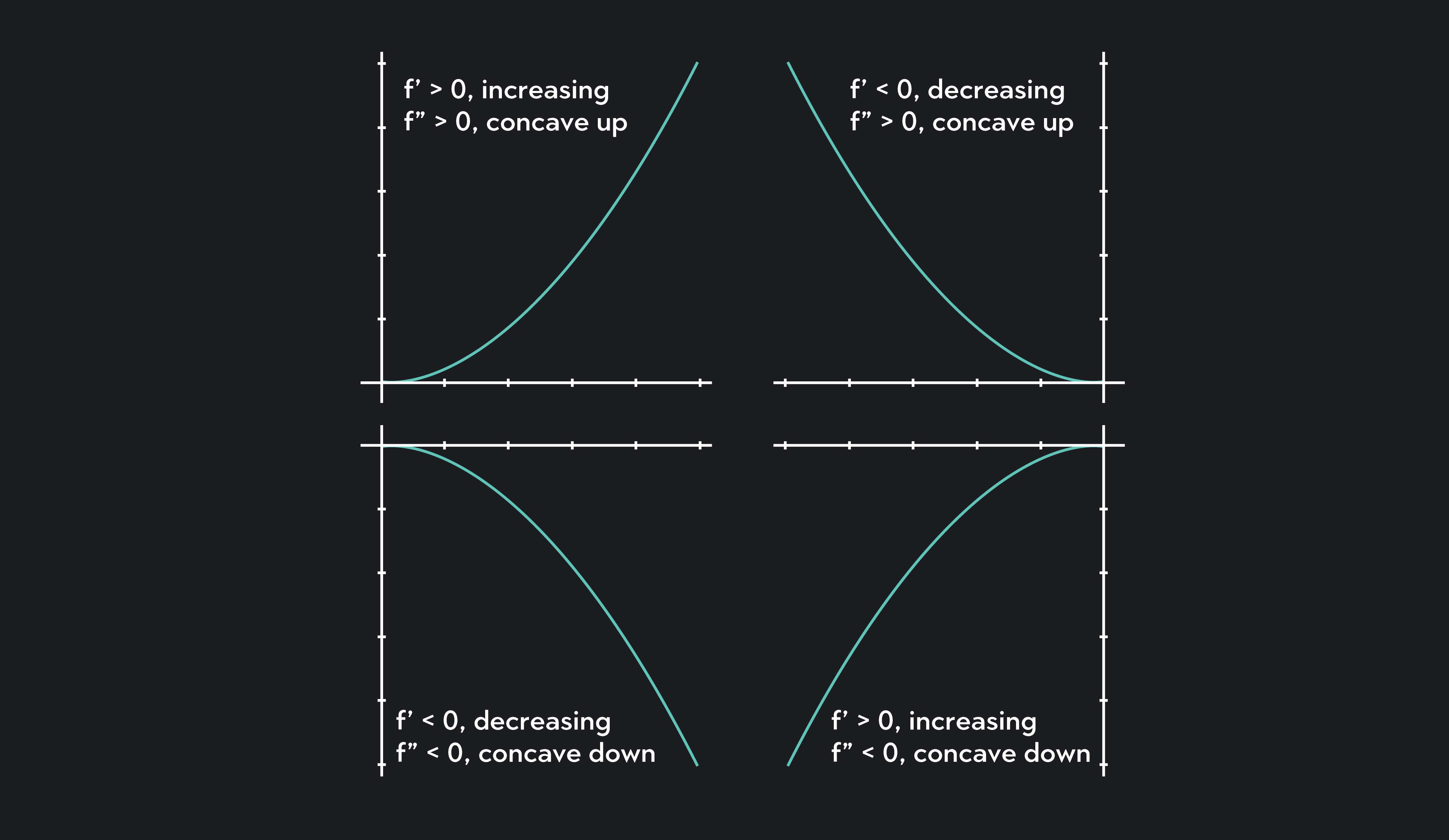
• Concave Up: The graph appears like a bowl, opening upwards, and the slope of the tangent lines increases as we move along the curve.
• Concave Down: The graph appears like an arch or dome, opening downwards, and the slope of the tangent lines decreases as we move along the curve.

Concavity plays a significant role in understanding the behavior of functions and is determined by the second derivative of the function. A positive second derivative indicates concave up, while a negative second derivative indicates concave down.

Why Is Concave Up or Down Important?

Understanding whether a function is concave up or down has multiple applications. It helps in identifying key features such as:

1. Critical points like maxima, minima, and points of inflection.
2. Predicting trends in data and optimizing mathematical models.
3. Providing insights into real-world phenomena, from economic models to physical systems.

For instance, in economics, concavity helps determine profit maximization or cost minimization. In physics, it aids in understanding motion and energy relationships. By analyzing concavity, professionals can make informed decisions and predictions.

How to Determine Concave Up or Down?

Determining whether a graph is concave up or down involves analyzing the second derivative of the function. Here's how you can do it:

1. Take the first derivative of the function to find its slope.
2. Take the second derivative of the function to determine the rate of change of the slope.
3. Analyze the sign of the second derivative:
   • If the second derivative is positive, the function is concave up.
   • If the second derivative is negative, the function is concave down.

Additionally, plotting the graph and observing its curvature can provide a visual confirmation of its concavity.

Read also:

Ultimate Guide To Understanding The Ny Mets Score

The Role of the Second Derivative

The second derivative, denoted as f''(x), plays a vital role in determining concavity. It measures the rate at which the slope of the tangent line changes. Here's a breakdown:

• If f''(x) > 0 for all x in an interval, the function is concave up in that interval.
• If f''(x)
• If f''(x) = 0, the function may have an inflection point, which is where concavity changes.

Understanding the second derivative not only helps in identifying concavity but also assists in sketching graphs and solving optimization problems.

Examples of Concave Up and Concave Down

Let’s look at some examples to solidify the concept:

• Concave Up Example: The function f(x) = x² is concave up for all x, as its second derivative, f''(x) = 2, is always positive.
• Concave Down Example: The function f(x) = -x² is concave down for all x, as its second derivative, f''(x) = -2, is always negative.

Real-world scenarios also provide examples of concavity. For instance, a profit curve in a business model might be concave down, indicating diminishing returns as production increases.

Applications in Economics

In economics, concavity is crucial for understanding concepts like marginal utility, cost functions, and profit maximization. A concave up cost function, for example, indicates economies of scale, while a concave down profit function shows diminishing returns.

Applications in Physics

Concavity is equally important in physics, where it helps explain motion, forces, and energy relationships. For instance, the trajectory of a projectile is typically concave down, representing the influence of gravity.

Applications in Engineering

Engineers use the concept of concavity to design structures, optimize systems, and analyze stress and strain. A concave up curve might indicate stability, while a concave down curve could signal potential failure points.

Real-World Illustrations

From the arches of bridges to the curves of roller coasters, concavity is visible everywhere. Understanding this concept helps in designing structures, analyzing data, and predicting trends effectively.

Common Misconceptions

One common misconception is that a curve being concave up or down depends solely on its direction. In reality, concavity is determined by the second derivative and not just the visual appearance of the graph.

How Do Inflection Points Relate to Concavity?

Inflection points occur where a graph changes concavity, from up to down or vice versa. These points are significant in understanding the overall behavior of a function and its real-world implications.

How to Change Concavity?

Changing concavity involves altering the second derivative of a function. This can be done by modifying the equation of the function or its parameters. Such changes have practical applications in optimizing systems and models.

Frequently Asked Questions

• What is the difference between concave up and convex? Concave up means the graph bends upwards, while convex generally refers to a similar property but is often used in geometry.
• Can a function be both concave up and down? Yes, but only over different intervals or at an inflection point.
• How do you find inflection points? Inflection points are found where the second derivative equals zero or does not exist, provided there’s a change in concavity.
• Is concavity related to slope? Indirectly, as concavity involves the second derivative, which is the rate of change of the slope.
• What are practical uses of concavity? Concavity is used in optimization, data analysis, economics, physics, and engineering.
• Does concavity impact integration? Yes, concavity can affect the interpretation of definite integrals and area under the curve.

Conclusion

Understanding "concave up or down" isn’t just a theoretical exercise—it’s a practical tool for interpreting graphs, optimizing systems, and making informed decisions in various fields. Whether you're a student or a professional, mastering this concept will undoubtedly enhance your analytical skills and problem-solving abilities. Remember, every curve tells a story, and concavity is the key to understanding it!