Mastering The Basics: How Do I Find Slope With Ease?
When it comes to understanding the fundamentals of mathematics, the concept of slope holds significant importance. Whether you're tackling algebra, graphing equations, or analyzing data trends, knowing how to find slope is a skill that can serve you well in both academic and real-world scenarios. But where should you start? For many, the idea of calculating slope can seem daunting, with its formulas and graphs creating an intimidating first impression.
Rest assured, finding the slope of a line is far simpler than it appears. With a clear understanding of the formula and its components—rise and run—you'll soon master this essential concept. Whether you're a student brushing up for an upcoming math test, a teacher looking for ways to simplify the topic for your students, or just someone curious about linear equations, this article will provide everything you need to know about finding slope.
From breaking down the slope formula step by step to exploring real-life applications, we aim to make the learning process engaging and straightforward. You'll find detailed explanations, illustrative examples, and answers to frequently asked questions to ensure a comprehensive understanding. So, let's dive in and uncover the simplicity of slope calculations!
Read also:Guiding Light 858 Angel Number Meaning And Its Profound Impact
Table of Contents
- What Is Slope?
- Why Is Slope Important?
- Understanding the Slope Formula
- How Do I Find Slope?
- What Does a Positive or Negative Slope Mean?
- How to Find Slope from a Graph?
- How to Find Slope from Two Points?
- Can Slope Be Zero?
- How to Find Slope of a Vertical or Horizontal Line?
- Real-Life Applications of Slope
- Common Errors to Avoid
- Tips and Tricks for Remembering Slope
- Frequently Asked Questions
- Conclusion
What Is Slope?
The slope of a line is a measure that describes its steepness, direction, and rate of change. Mathematically, slope is expressed as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line. In simpler terms, it tells you how much the line goes up or down for every step it moves horizontally.
In algebraic terms, slope is denoted by the letter m and is calculated using the following formula:
Slope (m) = Rise / Run = (Change in Y) / (Change in X) = (y₂ - y₁) / (x₂ - x₁)
Here, (x₁, y₁) and (x₂, y₂) are two points on the line. The slope can be positive, negative, zero, or undefined, depending on the orientation of the line.
Why Is Slope Important?
The concept of slope extends far beyond the classroom. In real-world situations, slope plays a vital role in various disciplines such as engineering, physics, economics, and even urban planning. For instance:
- In construction: Engineers use slope to design ramps, roads, and drainage systems.
- In science: The slope of a graph can indicate acceleration, speed, or other rates of change in experiments.
- In business: Slope helps analyze trends in sales, costs, and profits.
By understanding slope, you gain the ability to interpret data, predict outcomes, and make informed decisions in both academic and professional settings.
Read also:Chiefs Football Triumphs Traditions And Tactics
Understanding the Slope Formula
Before diving into calculations, it's crucial to comprehend the slope formula and its components. Here's a breakdown:
- Rise: The vertical change between two points, represented as the difference in their y-coordinates (y₂ - y₁).
- Run: The horizontal change between two points, represented as the difference in their x-coordinates (x₂ - x₁).
This formula is the foundation for determining slope, whether you're working with a graph, a table, or a set of points. It’s easy to memorize and apply once you understand its logic.
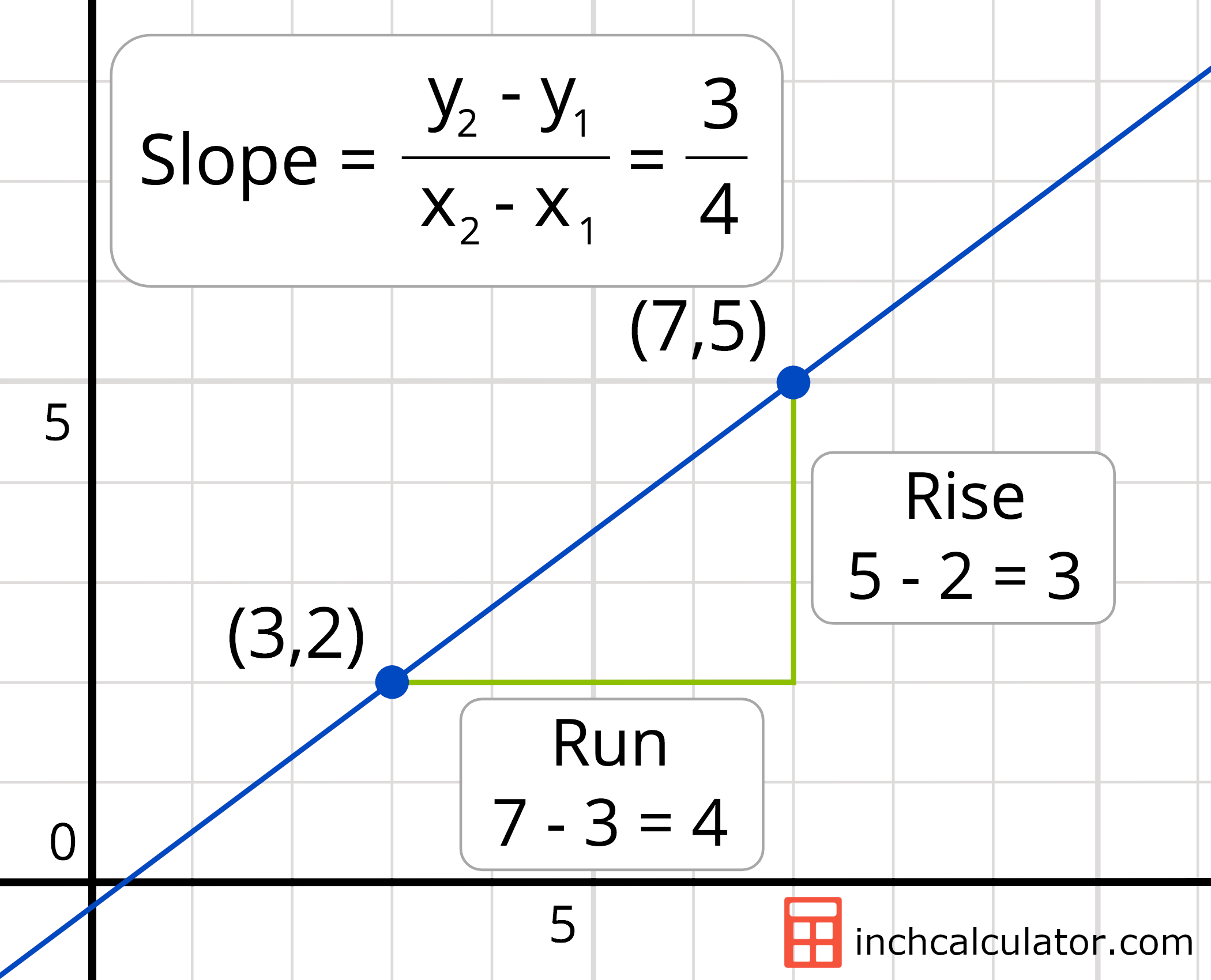
How Do I Find Slope?
Finding slope is a straightforward process when approached systematically. The key lies in identifying the rise and run, then plugging these values into the formula. Let’s break it down step by step.
Step-by-Step Guide to Calculating Slope
Here’s a simple guide to help you calculate the slope of a line:
- Identify two points on the line. Let these points be (x₁, y₁) and (x₂, y₂).
- Find the vertical change (rise) by subtracting y₁ from y₂.
- Find the horizontal change (run) by subtracting x₁ from x₂.
- Divide the rise by the run using the formula: Slope = (y₂ - y₁) / (x₂ - x₁).
- Simplify the result to find the slope.
For example, let’s calculate the slope of a line passing through the points (2, 3) and (6, 7):
- Rise = y₂ - y₁ = 7 - 3 = 4
- Run = x₂ - x₁ = 6 - 2 = 4
- Slope = Rise / Run = 4 / 4 = 1
So, the slope of the line is 1.
What Does a Positive or Negative Slope Mean?
The sign of the slope gives you information about the direction of the line:
- Positive Slope: The line rises as it moves from left to right.
- Negative Slope: The line falls as it moves from left to right.
If the slope is zero, the line is horizontal. If it’s undefined, the line is vertical.
How to Find Slope from a Graph?
To find the slope from a graph, follow these steps:
- Locate two points on the line.
- Draw vertical and horizontal lines to form a right triangle.
- Measure the rise and run.
- Use the formula Slope = Rise / Run.
How to Find Slope from Two Points?
This involves using the slope formula we discussed earlier. Simply substitute the coordinates of the two points into the formula and solve.
Can Slope Be Zero?
Yes, slope can be zero. This happens when the line is horizontal, meaning there’s no vertical change between the points.
How to Find Slope of a Vertical or Horizontal Line?
- Horizontal Line: Slope = 0 because rise = 0.
- Vertical Line: Slope is undefined because run = 0.
Real-Life Applications of Slope
Slope is widely used in real-world scenarios, such as designing roads, analyzing stock trends, and calculating speed.
Common Errors to Avoid
Some common mistakes include confusing rise and run, using incorrect points, and forgetting to simplify the slope.
Tips and Tricks for Remembering Slope
Use mnemonics like “Rise over Run” or practice with different examples to reinforce your understanding.
Frequently Asked Questions
- What is the formula for slope? The formula is (y₂ - y₁) / (x₂ - x₁).
- Can slope be negative? Yes, a negative slope indicates the line falls as it moves from left to right.
- What if the rise is zero? The slope is zero, indicating a horizontal line.
- What if the run is zero? The slope is undefined, indicating a vertical line.
- How is slope used in real life? Slope is used in engineering, economics, physics, and more for analyzing trends and designing structures.
- Can I find slope without a graph? Yes, you can use the slope formula with coordinates.
Conclusion
Understanding how to find slope is an essential skill in mathematics and beyond. By mastering the slope formula, interpreting its meaning, and applying it to real-world scenarios, you’ll gain a deeper appreciation for its utility. With practice and the tips provided in this article, finding slope will become second nature. So grab a pencil, start calculating, and watch as the world of linear equations unfolds before you!
Article Recommendations